Химическая энциклопедия
"ТЕМПЕРАТУРА"
Главная - Химическая энциклопедия - буква Т - ТЕМПЕРАТУРА
ТЕМПЕРАТУРА
(от
лат. temperatura- надлежащее смешение, нормальное состояние), термодинамич.
параметр, характеризующий состояние термич. равновесия макроскопич. системы.
Наряду с давлением, хим. потенциалом и др. параметрами состояния
, Т.
относится к интенсивным величинам, т.к. не зависит от массы системы. Согласно
принципу термич. равновесия, две фазы А и В, адиабатически изолированные от
окружающей среды (внутр. энергии фаз соотв. ЕА + ЕВ
= const), могут находиться в состоянии равновесия, к-рое характеризуется
определенными значениями Если две фазы с разл. q
приведены в тепловой контакт друг с другом через пов-сть раздела и qА
> qВ, возникает поток теплоты от А к В, т. е. от более
нагретой фазы к менее нагретой. При qА = qВ
тепловой поток отсутствует. Принцип термич. равновесия впервые сформулирован
Дж. Блэком в кон. 18 в. В термодинамику он введен, однако, позднее первого и
второго начал термодинамики, поэтому его часто называют нулевым началом термодинамики. Существует множество ф-ций
q(p, Понятие абсолютной Т. введено
У. Томсоном (лордом Кельвином) в 1848 на основании теоремы Карно, согласно к-рой
все обратимые тепловые машины, где рабочее тело совершает круговой процесс между
нагревателем с эмпирической Т. q1 и холодильником с эмпирической
Т. q2, имеют одинаковый кпд h, независимо от природы рабочего
тела: где Q1- тепло, отбираемое рабочим телом от нагревателя, Q2-тепло,
передаваемое холодильнику. Значения q1 и q2 можно
измерить с помощью произвольной шкалы Т., величины где T1
и Т2-абсолютные Т. нагревателя и холодильника соотв., причем
T1 есть ф-ция только q1, а Г2-только
q2. Для построения шкалы абсолютной Т. достаточно приписать
определенное значение Т, одному известному термич. состоянию. В настоящее время
по международному соглашению принято, что абсолютная (термодинамич.) Т. плавления
воды при нормальном давлении равна 273,15 К (точно). Абсолютный нуль Т. (или
нулевая абсолютная Т.) имеют ясный физ. смысл как Т. холодильника в цикле Карно,
при к-рой кпд тепловой машины h = 1. Тело, находящееся при нулевой Т.,
не способно передавать теплоту к.-л. другому телу. Единица измерения абсолютной
Т. в системе СИ-градус Кельвина (Кельвин, К). Конкретные измерения абсолютной
Т. осуществляются с помощью набора спец. термометров (подробнее см. Термометры
,
Термометрия
). Согласно строгой формулировке
второго начала термодинамики (аксиоматика Каратеодори), абсолютная Т. вводится
как интегрирующий делитель для бесконечно малого
кол-ва теплоты dQ, полученного системой, обладающей внутренней энергией Е, в обратимом процессе. Величина dQ/T
является полным дифференциалом ф-ции состояния S, наз. энтропией
. Абсолютная
Т. выражается соотношением: X1, X2,
Х3, ...-экстенсивные термодинамич. переменные (объем V,
электростатич. индукция D, магн. индукция В и т.п.). Абсолютная
Т. и эмпирическая Т. q связаны аналит. зависимостью для систем, у к-рых
E является ф-цией только Ти V: Аналит. связь p, где W— термодинамич.
вероятность, k-постоянная Больц-мана. Термодинамич. вероятность W(E)равна числу возможных состояний системы, при к-рых последняя обладает внутр.
энергией Е. Термодинамич. вероятность связана с энтропией соотношением
Больцмана S = kln W. Для обычной макроскопич. системы величина
W- быстро возрастающая ф-ция Е и, следовательно, абсолютная Т.
положительна. Термич. равновесие двух
систем А и В (EА + ЕB = const), определяемое
равенством т-р TА = ТB, соответствует наиб.
вероятному распределению энергии между А и В. Если В представляет собой обширный
тепловой резервуар (ЕВ >> EА),
то абсолютная Т. определяет плотность вероятности Р(Е) для
системы А находиться в состоянии с заданной энергией EA,r
при термич. равновесии с системой В: где, суммирование ведется
по всем значениям
Важные физ. постоянные
в-ва-его Т. кипения, плавления, фазовых переходов, полиморфных превращений,
а также критическая Т. (см. Критическое состояние
), тройные точки
. Практически все физ.-хим.
величины зависят от Т. Важными примерами являются температурные зависимости: 1) константы скорости хим.
р-ции к: где EA-энергия
активации, A-предэкспоненциальный множитель (см. Аррениуса уравнение
,
Константа скорости
, Энергия активации
). 2) Константы равновесия
хим. р-ции Кр: где R-газовая постоянная,
3) Теплового эффекта хим.
р-ции при постоянном давлении (DH) и постоянном объеме (DU): (9DН/9Т)р
= DСр, (9DU/9Т)V
= DСV, где H и U-энтальпия
и внутр. энергия системы, Ср и СV-теплоемкости
при постоянном давлении и постоянном объеме соотв. (см. Кирхгофа уравнение
). 4) Теплоты равновесного
фазового перехода L: где 5) Стандартной электродвижущей
силы E0 гальванич. цепи: где Кр(Т)-константа
равновесия электродного процесса, F-Фарадея постоянная, Z-число
переносимых электронов (см. Электрохимические цепи
). 6) Объемной плотности rv
излучения абсолютно черного тела с частотой v (ф-ла Планка): где с-скорость света,
h-постоянная Планка. Полной объемной плотности
излучения по всем частотам (закон
Стефана - Больцмана): 7) Степени ионизации a
газа, состоящего из атомов А: где Ei-энергия
ионизации атома, m-масса электрона; gi, gА-статистич.
веса ионов и атомов (ур-ние Саха). Понятие Т., сформулированное
для равновесного состояния системы в целом, используется и для характеристики
локального термодинамич. равновесия, если система в целом неравновесна и ее
Т. рассматривается как непрерывная ф-ция координат и времени. При локальном
термодинамич. равновесии малые элементы объема приближенно рассматриваются как
равновесные, обладающие каждый своей Т., и учитывается обмен энергией (энтропией)
между ними. Локальное термодинамич. равновесие-одно из осн. понятий термодинамики необратимых процессов
. В ряде физ. задач неравновесная система м. б. разбита
на подсистемы, в к-рых время установления термич. равновесия много меньше времени
достижения равновесия системой в целом. Подобная ситуация м. б. охарактеризована
тем, что каждой из подсистем соотносится своя Т., отличная от Т. других подсистем.
Напр., в полупроводниках Т. электронов проводимости в сильном электрич. поле
много выше Т. решетки; в плазме отдельно рассматривают Т. электронов и Т. ионов. В нач. 50-х гг. 20 в. сформулировано
понятие отрицательных абсолютных Т. Такие Т. могут возникать в системах, если
с ростом энергии Е термодинамич. вероятность W (или энтропия S)не возрастает, а убывает, в результате
чего производная При физ.-хим. исследованиях
условно выделяют область низких Т. (см. Криохимия
) и область высоких
Т. (обычно 500-3000 К), к-рую рассматривают как химию высоких Т., или просто
высокотемпературную химию. Т. в интервале 500-3000 К получают методами радиационного
и лазерного нагрева, электронной и ионной бомбардировки. Объекты высокотемпературной
химии, как правило,-неорг. соединения. Характерными чертами высокотемпературных
хим. процессов являются: 1) сравнительно малая роль констант скорости, энергий
активации и т. п. кинстич. факторов, поскольку скорость р-ций высока и в системе
быстро устанавливается равновесие; 2) увеличение роли газовой (паровой) фазы
из-за интенсивных процессов испарения; 3) необходимость учета влияния заряженных
частиц-ионов и электронов, возникающих в результате термодиссоциации (см. Ионы в газах
, Ионно-молекулярные реакции
). Высокотемпературными процессами
являются мн. металлургич. произ-ва, процессы напыления пленок, монокристаллов выращивания
из газовой фазы и др. Процессы в области Т. 3000-5000
К изучаются плазмо-химией. Лит.: Кричевский
И. Р., Понятия и основы термодинамики, 3 изд., М., 1962; Рей Ф., Статистическая
термодинамика, пер. о англ., М., 1986. М. В. Коробов.
|
Поделитесь с друзьями:
Вы можете поставить ссылку на это слово:
будет выглядеть так: ТЕМПЕРАТУРА
будет выглядеть так: Что такое ТЕМПЕРАТУРА
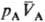 и
и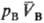 (рА,
рB-давления;
(рА,
рB-давления;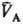 ,
,
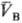 -молярные объемы фаз). Экспериментально установлено, что если фаза А находится
в равновесии с фазой В, а В-с С, то А и С также находятся в равновесии. Из принципа
термич. равновесия следует, что каждая фаза обладает эмпирической Т. q-измеримым
св-вом такого рода, что из qА(рA;
-молярные объемы фаз). Экспериментально установлено, что если фаза А находится
в равновесии с фазой В, а В-с С, то А и С также находятся в равновесии. Из принципа
термич. равновесия следует, что каждая фаза обладает эмпирической Т. q-измеримым
св-вом такого рода, что из qА(рA;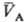 )
= qB(рB;
)
= qB(рB;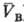 )
и qB(рB;
)
и qB(рB;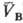 )
= qC(рC;
)
= qC(рC;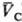 )
следует qА(pА;
)
следует qА(pА;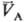 )
= qс(рс;
)
= qс(рс;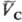 ).
).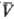 ),
удовлетворяющих нулевому началу. Конкретный вид q(p,
),
удовлетворяющих нулевому началу. Конкретный вид q(p,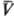 )
определяется используемым измерит. прибором-термометром и способом построения
термометрич. шкалы.
)
определяется используемым измерит. прибором-термометром и способом построения
термометрич. шкалы.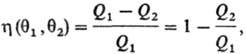
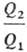 и
h при смене шкалы остаются постоянными. Абсолютная Т. вводится соотношением:
и
h при смене шкалы остаются постоянными. Абсолютная Т. вводится соотношением: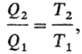
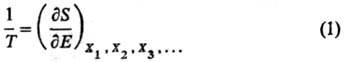
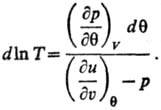
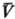 и
Т для фазы наз.
и
Т для фазы наз. 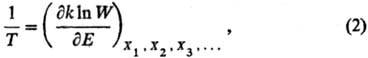
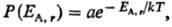
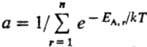 энергии EA.r
(r = 1,2,... , п) подсистемы А (канонич. распределение
Гиббса). Частными случаями канонич. распределения являются распределения молекул
идеального газа по энергиям и скоростям (распределения Больцмана и Максвелла).
энергии EA.r
(r = 1,2,... , п) подсистемы А (канонич. распределение
Гиббса). Частными случаями канонич. распределения являются распределения молекул
идеального газа по энергиям и скоростям (распределения Больцмана и Максвелла).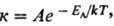
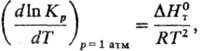
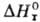 -стандартная
энтальпия р-ции.
-стандартная
энтальпия р-ции.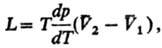
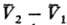 -изменение
молярного объема при переходе в-ва
из фазы 1 в фазу 2 (см.
-изменение
молярного объема при переходе в-ва
из фазы 1 в фазу 2 (см. 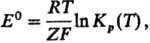
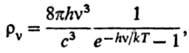
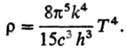
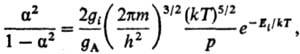
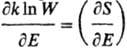 становится меньше
нуля (см. ф-лы 1 и
становится меньше
нуля (см. ф-лы 1 и