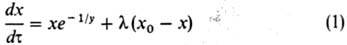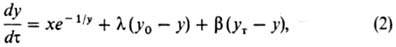Химическая энциклопедия
"РЕАКТОРЫ ХИМИЧЕСКИЕ"
Главная - Химическая энциклопедия - буква Р - РЕАКТОРЫ ХИМИЧЕСКИЕ
РЕАКТОРЫ ХИМИЧЕСКИЕ
(от
лат. rе- приставка, означающая обратное действие, и actor - приводящий в действие,
действующий), пром. аппараты для осуществления хим. р-ций. Конструкция и режим
работы Р. х. определяются типом р-ции, фазовым состоянием реагентов, характером
протекания процесса во времени (периодический, непрерывный, с изменяющейся активностью
катализатора), режимом движения реакц. среды (периодический, полупроточный,
с рециклом), тепловым режимом работы (адиабатический, изотермический, с теплообменом),
типом теплообмена, видом теплоносителя. По типу конструкции Р. х. подразделяют
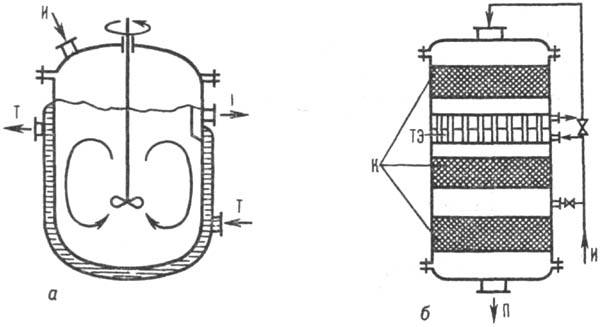
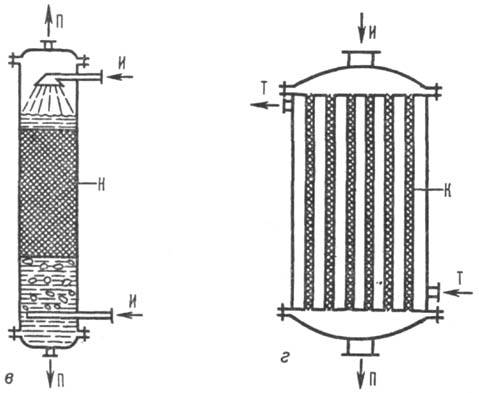
на емкостные, колонные, трубчатые (рис. 1). Емкостные Р. х.-полые аппараты,
часто снабженные перемешивающим устройством. Перемешивание газо-жидкостных систем
может производиться барботированием
газообразного реагента. Теплообмен
осуществляется через пов-сть Р. х. или путем частичного испарения жидкого компонента
реакц. смеси. К реакторам этого типа относят также аппараты с неподвижным или
псевдоожиженным слоем (одним или несколькими) катализатора (см., напр., Псевдоожижение
).
В многослойных реакторах теплообмен осуществляется смешением потоков реагентов
или в теплообменных элементах аппарата. В емкостных Р. х. проводят непрерывные,
перио-дич. и полупериодич. процессы (см. Непрерывные и периодические процессы
). Рис. 1 Основные типы хим.
реакторов: а-проточный емкостный реактор с мешалкой и теплообменной рубашкой;
б - многослойный каталитич. реактор с промежуточными и теплообменными
элементами; в-колонный реактор с насадкой для двухфазного процесса; г-трубчатый
реактор; И-исходные в-ва; П- продукты р-ции; Т - теплоноситель; К - катализатор;
Н-насадка; ТЭ теплообмен-ные элементы. Колонные Р.х. могут быть
пустотелыми либо заполненными катализатором или насадкой (см. Насадочные аппараты
). Для улучшения межфазного массообмена применяют диспергирование
с помощью разбрызгивателей (см. Распыливание), барботеров, мех.
воздействия (вибрация тарельчатой насадки, пульсация потоков фаз) или насадки,
обеспечивающей высокоскоростное пленочное движение фаз. Р.х. данного типа используют
в осн. для проведения непрерывных процессов в двух- или трехфазных системах.
Трубчатые Р.х. применяют часто для каталитич. р-ций с теплообменом в реакц.
зоне через стенки трубок и для осуществления высокотемпературных процессов газификации.
При одновременном скоростном движении неск. фаз в таких реакторах достигается
наиб. интенсивный межфазный массообмен. Специфич. особенностями отличаются Р.
х. для электрохим. (см. Электролиз
), плазмохим. (см. Плазма-химическая технология) и радиационно-хим. (см. Радиацион-но-химическая технология)
процессов. При расчете Р. х. определяют
необходимые для достижения заданной производительности и селективности процесса
объем аппарата, скорость потока, пов-сть теплообмена, гидравлич. сопротивление,
режим работы, конструктивные параметры (уточняются на основании аэродинамич.
испытаний). Расчет выполняют на основе данных по термодинамике и кинетике р-ций,
скорости тепло- и массообмена (см. Макрокинетика
)с учетом структуры потоков
в аппаратах. Наиб. полный расчет, проводимый методом моделирования с использованием ЭВМ, включает определение полей т-ры и концентрации, оптим.
режима, схемы теплообмена и циркуляции (см. Оптимизация
), а также,
наряду с выбором способа управления, анализ устойчивости режима. См. также Массообмен
,
Перемешивание
, Печи
, Пленочные аппараты
, Теплообмен
. Лит.: Левеншпиль
О., Инженерное оформление химических процессов пер. с англ., М., 1969; Дидушинский
Я., Основы проектирования каталити ческих реакторов, пер. с польск., М., 1972;
Расчет химико-технологических процессов, под ред. И. П. Мухленова, Л., 1976;
Общая химическая технология, ч. 1. Теоретические основы химической технологии,
4 изд., М., 1984, с. 77-119 Кутепов А. М., Бондарева Т. И., Беренгартен М. Г.,
Общая химичес кая технология, 2 изд., ч. 1, М., 1990, с. 63-169. B.C. Бесков Динамические режимы
хим. реакторов характеризуются изменением во времени параметров, определяющих
состояние процесса (концентрация, т-ра, давление и др.). В дина-мич. режиме
всегда функционирует реактор периодич. действия, в к-ром ход процесса изменяется
от момента загрузки сырья до выгрузки готового продукта. Реактор непрерывного
действия должен работать в стационарном, неизменном во времени режиме. Однако
из-за неизбежных внеш. возмущений, напр. изменения состава сырья, условий отвода
или подвода теплоты, возникают отклонения от стационарного режима. Они м. б.
незначительными и существенными, приводящими к заметным изменениям качества
продукта, производительности реактора и даже к авариям. Динамич. режимы реакторов
непрерывного действия исследуют с помощью их мат. моделей в виде диффе-ренц.
ур-ний в обыкновенных или частных производных. Динамич. режимы непрерывно
действующего реактора идеального смешения, в к-ром протекает экзотермич. р-ция
первого порядка, описываются безразмерной системой ур-ний, составленной на основе
материального (1) и теплового (2) балансов: где х, у -переменные,
пропорциональные соотв. концентрации реагирующего в-ва и т-ре в реакторе; x0,
y0-те же переменные для потока на входе реактора; ут
- переменная, пропорциональная т-ре окружающей среды; l-констан та,
пропорциональная расходу потока на входе реактора, b-константа, пропорциональная
коэф. теплопередачи и площади
пов-сти теплообмена с окружающей средой; т-время. Стационарные режимы реактора
определяются условием dx/dт = dy/dт =
0. Решение ур-ний (1), (2) при этом дает значения xs и ys
для стационарного состояния. В зависимости от параметров реактора стационарных
состояний м. б. одно или три; в общем случае их всегда нечетное число. Динамич. режимы исследуют
с помощью фазовой плоскости x, у. Решения системы (1), (2) являются
ф-циями времени х(т), y(т) и начальных условий.
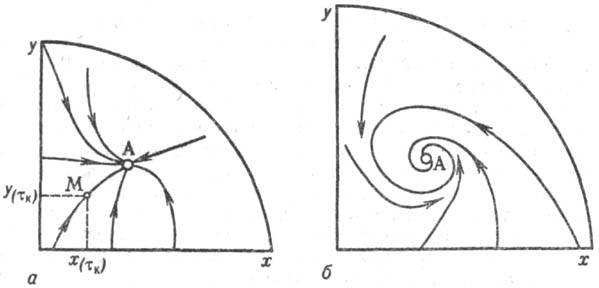
Каждому мгновенному состоянию реактора (рис. 2) в момент тк
соответствует на плоскости х, у нек-рая точка М, наз. изображающей. При
изменении т эта точка будет двигаться по фазовой плоскости; траектория точки
наз. фазовой. Вся совокупность траекторий, отвечающих разл. начальным условиям,
представляет собой фазовый портрет системы, к-рый однозначно отражает динамич.
режимы. Стационарные состояния
реактора изображены на фазовых портретах спец. точками (А, В, С). Направление
изменения режима реактора указывается стрелками. Если траектория стремится к
стационарному состоянию, то оно устойчиво, а режим реактора работоспособен.
Если траектория выходит из стационарного состояния, то оно неустойчиво. Исследования
устойчивости стационарных состояний - одна из главных задач изучения динамич.
режимов. На рис. 2 представлены
фазовые портреты системы, отражающие наиб. интересные динамич. режимы функционирования
хим. реакторов. Портрет а соответствует режиму с единств. устойчивым
стационарным состоянием А, при отклонении от к-рого переменные х и у стремятся в него вернуться. Спиральный характер траекторий на портрете б означает, что режим приближения к единств. стационарному состоянию А является
колебательным затухающим. Траектории на портрете
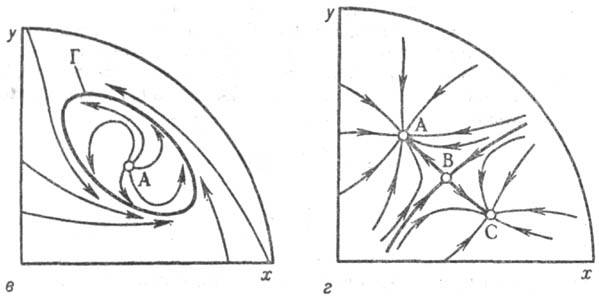
в, отвечающие неустойчивому стационарному состоянию А, уходят от него
и стремятся к замкнутой траектории Г, наз. предельным циклом. Движение изображающей
точки по Г означает незатухающие колебания х и у. Исследования
таких режимов (автоколебаний)-еще одна задача изучения динамич. режимов. Портрет
г соответствует режиму с тремя стационарными состояниями, одно из к-рых неустойчиво.
Принципиально возможен случай, когда все стационарные состояния неустойчивы.
При этом они охватываются предельным циклом. Изучение динамич. режимов позволяет
решать проблемы оптим. конструирования и автоматизации хим. реакторов. Рис. 2. Фазовые портреты
хим. реакторов: а-устойчивый режим с монотонным приближением к единств.
стационарному состоянию А; б-устойчивый режим с колебат. приближением
к состоянию А; в-автоколебат. режим, от стационарного состояния А режим
переходит на предельный цикл Г; г-случай трех стационарных состояний,
из к-рых А и С устойчивы, В-неустойчиво. Лит.: Вольтер Б.
В., Сальников И. Е., Устойчивость режимов работы химических реакторов, 2 изд.,
М., 1981; Aris R., Mathematical modelling techniques, S. F., 1979. Б. В.
Вольтер. |
Поделитесь с друзьями:
Вы можете поставить ссылку на это слово:
будет выглядеть так: РЕАКТОРЫ ХИМИЧЕСКИЕ
будет выглядеть так: Что такое РЕАКТОРЫ ХИМИЧЕСКИЕ