Химическая энциклопедия
"РАСТВОРЫ ЭЛЕКТРОЛИТОВ"
Главная - Химическая энциклопедия - буква Р - РАСТВОРЫ ЭЛЕКТРОЛИТОВ
РАСТВОРЫ ЭЛЕКТРОЛИТОВ
,
содержат в заметных концентрациях ионы-катионы и анионы, образующиеся в результате
электролитической диссоциации
молекул растворенного в-ва. Р-ритель (чистый
или смешанный) обычно в сколько-нибудь значит. степени не диссоциирован. Р.
э. обладают способностью проводить электрич. ток и относятся к проводникам второго
рода. Благодаря увеличению общего числа частиц коллигативные св-ва бесконечно
разбавленных Р. э.
(т. е. св-ва, зависящие только от концентрации растворенного в-ва, но не от
его природы) существенно отличаются от тех же св-в растворов неэлектролитов
.
Этим, в частности, объясняется увеличение осмотич. давления в сравнении
со значением, предсказываемым законом Вант-Гоффа (см. Осмос
), понижение
давления пара р-рителя над р-ром в сравнении с предсказываемым Рауля законом
и др. Наличием ионов обусловлены также классификация Р.э., особенности теоретич.
подходов в сравнении с др. классами р-ров. Наиб. изучены водные Р.э., играющие
важную роль во многих биол., геол. и техн. процессах. Неводные Р.э. служат средой
для проведения синтеза и электрохим. процессов, используются в совр. технологиях
(создание новых химических источников тока, солнечных батарей, процессы
разделения в-в и др.). Классификация Р.э. основана
на классификации электролитов. Соответственно о Р.э. говорят как о симметричных
и несимметричных в зависимости от того, распадается ли молекула растворенного
в-ва в р-ре на два иона или на большее число частиц; z, z-зарядных [напр.,
р-р NaCl 1,1-зарядный, р-р СаС12 2,1-зарядный] и т.п.-По степени
диссоциации электролита a, к-рая равна отношению числа молекул, диссоциированных
на ионы, к полному числу молекул в р-рс, различают сильные (a = 1), слабые
(a << 1) электролиты и, соотв., р-ры сильных и слабых электролитов.
Такое деление, однако, является условным и отражает состояние электролита в
р-ре, определяемое не только природой растворенного в-ва и р-рителя, но и концентрацией
(молярной долей хэл), т-рой Т, давлением р. В зависимости от состояния
растворенного в-ва до растворения выделяют два класса Р.э.-р-ры ионофоров и
р-ры ионогенов. Ионофоры в чистом состоянии существуют в виде ионных кристаллов
(напр., галогениды щелочных металлов). В сильнополярных р-рителях (напр., в
воде) ионофоры, как правило, диссоциируют полностью и составляют р-ры сильных
электролитов. В слабополярных р-рителях (напр., в уксусной к-те) они образуют
р-ры слабых электролитов. Ионогены до растворения состоят из молекул, они являются
потенц. электролитами, электролитич. диссоциация проходит, как правило, в две
стадии и обычно не полностью (хлорная к-та в уксусной к-те). Растворители для Р.э-как
правило, полярные жидкости (чистые или смешанные). Чем больше диэлектрич. проницаемость
e р-рителя, тем значительнее ослабляется сильное электростатич. притяжение
противоположно заряженных ионов, что способствует возникновению в р-ре ионов.
Интенсивное взаимод. последних с молекулами р-рителя приводит к связыванию ионов
с молекулами р-рителя (см. Сольватация
). Важна также способность молекул
р-рителя выступать в качестве доноров или акцепторов протонов или электронов.
В зависимости от этих двух св-в различают четыре группы р-рителей: 1) протонные
р-рители (вода, спирты, карбоновыс к-ты и др.), к-рые являются хорошими донорами
протона и обладают высокой диэлектрич. проницаемостью (e > 15); 2) апротонные
дшюлярные р-рители (нек-рые апротонные амиды, кстоны, сульфоксиды и др.), обладающие
высокой диэлектрич. проницаемостью, но не обладающие донорно-акцепторными св-вами
в отношении протона; 3) электронодонорные-р-рители (напр., эфиры); 4) неполяр-ныс
р-рители (сероуглерод, углеводороды), к-рые обладают низкой диэлектрич. проницаемостью
(e < 15) и не обладают донорно-акцепторными св-вами ни по отношению
к протону, ни по отношению к электрону. Находящиеся в Р. э. ионы
могут существовать в виде своб. сольватир. ионов или в виде ассоциатов-контактных
или сольватно разделенных ионных пар, тройников и т.д. Поскольку ионные пары
не проводят электрич. ток, содержание своб. ионов в Р. э. определяется по его
электрич. проводимости, в то время как общее число ионов (свободных и ассоциированных)
можно определить, напр., спектрофотомет-рич. методами. Термодинамика Р. э. Равновесные
тсрмодинамич. св-ва Р.э. описываются парциальными молярными величинами
,
в к-рых различают
катионные и анионные вклады. Напр., для электролита типа где v=v++v_,
x+ и х--молярные доли катионов и анионов
соотв., средняя молярная доля электролита хb = = Др. парциальные молярные
величины связаны с mэл термо-динамич. соотношениями: парциальная
молярная энтропия Sэл = -(9mэл/9Т)p,
парциальная молярная энтальпия Hэд_= = -Т2[(9mэл/Т)/9Т]р,
теплоемкость Ср = -Т(92mэл/9Т2)p,
парциальный молярный объем Vэл = (9mэл/9р)T. В качестве стандартного состояния
компонентов в Р.э. выбирают: для р-рителя-состояние чистой жидкости,
для растворенного в-ва-состояние в гипотетич. р-ре, где его концентрация и активность
равны единице, а термодинамич. св-ва В электролитах с неполной
степенью диссоциации (а < 1) выражение (1) заменяется соотношением: где где
Для описания отклонения
от идеального состояния разбавленных Р.э. используют кажущиеся осмотические
коэффициенты, характеризующие
отклонение осмотич.
давления от значения, определяемого законом Вант-Гоффа, и связанные с ионными
коэф. активности соотношением: где m - моляльность
электролита, gb-ионные коэф. активности в моляльной шкале,
MS-молярная масса (кг·моль-1), xS-молярная
доля р-рителя. Хим. потенциалы mэл,
коэф. активности gb и осмотич. коэффициенты Ф м. б. определены
экспериментально прямыми или косвенными методами: по давлению пара растворенного
в-ва или р-рителя, по р-римости, по измерениям эдс электролитич. цепи. Из калориметрич.
экспериментов находят парциальную молярную энтальпию Hэл,
а из измерений плотности-парциальные молярные объемы Vэл.
Поскольку измеримы только суммарные термодинамич. характеристики электролита,
для катионов и анионов хим. потенциалы m+ и m_,
их стандартные значения Наряду с хим. потенциалами
ионов используют также электрохим. потенциал i-го иона с валентностью
zi: где F-Фарадея постоянная,
f-внутр. электрич. потенциал Р.э. (см. Межфазные скачки потенциала
). Статистические теории Р.э.
основаны на методах стати-стич. механики, их осн. задача-расчет св-в исходя
из энергии межчастичного взаимодействия. Развиваются след. подходы: ионный подход
(уровень Макмиллана-Майера); ион-но-молекулярный подход (уровень Борна-Оппенгеймера);
электрон-ядерный подход (уровень Шрёдингера ). Ионный подход является традиционным
и к настоящему времени наиб. развит. Он основан на рассмотрении в явном виде
только ионов, р-ритель из явного рассмотрения исключается, что требует усреднения
ф-ции распределения Гиббса по всем мол. конфигурациям р-рителя (см. Статистическая термодинамика
). Энергия межионного взаимод. представляется как сумма слагаемых
унарного, бинарного, тернарного и т.д. типов. Унарные слагаемые выражаются через
своб. энергию сольватации Wi i-го иона, характеризуемую изменением
энергии Гиббса системы при переносе иона из идеальной газовой фазы в бесконечно
разб. р-р. Значение Wi совпадает с неидеальной частью стандартного
хим. потенциала i-го иона, причем выделяют электростатич., неэлект-ростатич.
и хим. вклады в значение Wi. Электростатич. вклад Wiэл
м. б. рассчитан согласно модели Борна, в рамках к-рой р-ритель рассматривается
как бесструктурная среда, характеризуемая диэлектрич. проницаемостью e: где e0-диэлектрич.
постоянная (диэлектрич. проницаемость вакуума), ri-ионный
радиус (см. Атомные радиусы
). Для уточнения расчета вместо радиуса
ri используется эффективный радиус К неэлектростатич. вкладам
в Wi относят индукционный и дисперсионный вклады (см. Дисперсионное взаимодействие
), а также вклад, связанный с работой, к-рую необходимо
затратить для образования в р-рителе полости и внедрения в нее иона. Расчет
этих вкладов производится теми же методами, что и для р-ров неэлектролитов.
Для расчета энергии сольватации применяют квантовохим. методы. Бинарные слагаемые в энергии
межионного взаимод. выражаются через потенциалы Wij(R),
описывающие эффективное взаимод. ионов сортов i и j, находящихся
на расстоянии R друг от друга. Соотв. тернарные слагаемые выражаются
через потенциалы, описывающие трехчастичное взаимод. ионов и т. д. Учет бинарных
и высших слагаемых в выражении для энергии межионного взаимод. позволяет описывать
концентрац. зависимости термодинамич. св-в Р.э. Св-ва Р.э. характеризуются
сложными концентрац. зависимостями, обусловленными конкуренцией вкладов разл.
типов межчастичных взаимодействий. Обычно ограничиваются учетом потенциалов
парного взаимодействия. Его существ. особенность-кулоновский характер межионного
взаимод. на больших расстояниях (при С кулоновским взаимод.
связано экранирование межионных взаимод. и образование ионных комплексов, эти
процессы характеризуются
соотв. радиусом Дебая rD = С увеличением концентрации
электролита возникает необходимость учитывать и некулоновскую часть межионного
взаимод., для чего прибегают к нек-рым моделям. При этом наряду с индукционным,
дисперсионным, обменным и др. видами межчастичных взаимод. некулоновский потенциал
учитывает сольватац. эффекты, связанные с влиянием р-ри-теля. В частности, учет
некулоновской части взаимод. стабилизирует уменьшение коэф. активности ионов
с концентрацией и может объяснить их увеличение, наблюдаемое экспериментально.
Наипростейшей ионной моделью Р. э. является модель заряженных твердых сфер (т.
наз. примитивная модель). Первые попытки описания примитивной модели были выполнены
в рамках теории Дебая-Хюккеля (второе приближение). Более корректно учет размера
ионов и неку-лоновского взаимод. осуществляется на основе методов статистич.
термодинамики (см. Жидкость
). В рамках примитивной модели
размеры ионов отличаются от кристаллографич. радиусов из-за сольватац. эффектов.
Однако даже при одном и том же выборе размеров ионов удовлетворительно описать
эксперим. результаты для разл. термодинамич. св-в Р. э. в примитивной модели
оказалось затруднительным. К более корректным результатам приводит модель парного
взаимод. типа "прямоугольной ямы", в к-рой ширина потенц. ямы выбирается
равной диаметру молекулы р-рителя, а глубина ямы считается подгоночным параметром,
учитывающим сольватац. эффекты; при этом используются кристаллографич. размеры
ионов. В более реалистич. модели Фридмана в некулонов-ском потенциале межионного
взаимод. выделяют три слагаемых, соответствующих: 1) главному отталкиванию ионов,
определяемому их кристаллографич. размерами; 2) эффекту поляризации полости
ионов р-рителем; 3) потенциалу Гер-ни-Франка, описывающему структурные эффекты,
связанные с перекрыванием сольватных оболочек ионов при их сближении. Расчеты
на основе ион-молекулярных моделей показывают, что на малых расстояниях межионные
потенциалы имеют отталкивательный характер, на больших расстояниях, в соответствии
с (7), зависят от расстояния между ионами асимптотически, как и при кулоновском
взаимод., на промежут. расстояниях осциллируют вблизи этой асимптоты, причем
с уменьшением размера иона (или с увеличением его валентности) амплитуда осцилляции
возрастает, что соответствует усилению роли сольватац. эффектов. Пренебрежение трехчастичными
(и высшими) межионными взаимод. ограничивает возможности ионного подхода. В
частности, для 1,1-зарядных водных Р. э. ионный подход обеспечивает количеств.
описание термодинамич. св-в в области концентраций до 1 М. Учет концентрац.
зависимости диэлектрич. проницаемости позволяет немного расширить эту концентрац.
область. Формально расширения области применимости ионного подхода можно достигнуть,
дополняя полученные с его помощью результаты разл. эмпирич. поправками. Примером
такого подхода может служить полуэмпирич. ур-ние Питцера для осмотич. коэффициента
или метод Робинсона-Стокса описания ионных коэф. активности с учетом гидратации
(с помощью гидра-тац. чисел). Для описания многокомпонентных Р. э. широко используется
правило Здановского, основанное на предположении
о том, что смешение изописстич. р-ров разл. электролитов, химически не взаимодействующих
между собой, происходит без изменения активности р-рителя. Ионно-молекулярный подход
основан на рассмотрении в явном виде как ионов, так и молекул р-рителя. Главные
результаты получены в 70-80-х гг. 20 в. на базе расчетных методов, интенсивно
развиваемых в теории жидкостей. Это в осн. метод интегральных ур-ний для корреляц.
ф-ций, метод кластерных разложений, теория возмущений, а также компьютерное
моделирование. Благодаря явному учету ионно-молекулярных и межмолекулярных взаимод.
возможно описание не только термодинамич., но и структурных св-в Р. э. В частности,
важный результат - описание сольватации ионов в зависимости от концентрации
и др. параметров р-ра, объяснение концентрационных, температурных и барич. зависимостей
св-в в широких интервалах состава, т-ры и давления. Наипростейшей ион-молекулярной
моделью Р. э. является ион-дипольная модель, в к-рой ионы рассматриваются как
заряженные твердые сферы, а молекулы р-рителя моделируются твердыми сферами
с дипольным моментом. Полученные выражения для термодинамич. ф-ций обобщают
ур-ния, используемые в ионном подходе. В частности, в предельном случае малых
концентраций выражения для ионных коэф. активности включают члены, основанные
на теории Дебая-Хюккеля, а выражения для энергии сольватации-борновскую ф-лу
(6) с эффективным радиусом иона Предпринимаются попытки
учета квадрупольного элект-рич. момента и поляризуемости
молекул р-рителя,
а также взаимод., ответственных за образование в Р. э. ассоциатов и сольватов.
Наиб. реальные модели разработаны в осн. для водных Р. э. и базируются обычно
на компьютерном моделировании. Для описания ионно-молекулярных и межмолекулярных
взаимод. применяют эмпирич. модели воды (модель ST2, модель центр.
сил и др.), а также модели, основанные на квантовохим. расчетах. Рассчитанные
парциальные радиальные ф-ции распределения дают информацию о структуре р-ра.
В частности, с помощью ионно-молекулярных ф-ций определяют координац. числа
сольватации. Найденные с помощью парциальных радиальных ф-ций структурные факторы
удовлетворительно согласуются с данными дифракц. измерений. Электрон-ядерный подход
основан на учете электроста-тич. взаимод. между электронами и ядрами, входящими
в состав ионов и молекул в Р. э. Этот подход является наиб. последовательным,
он основан на квантовомех. рассмотрении и разработан пока лишь для ион-молекулярных
комплексов. Важное значение в физ.
химии Р. э. имеют исследования транспортных св-в, особенно электрич. проводимости
(см. Электропроводность электролитов
). Наличие ионов заметно сказывается
на диффузии, вязкости, теплопроводности. Лит.: Робинсон Р.
А., Стоке Р. Г., Растворы электролитов, пер. с англ., М., 1963; Измайлов Н.А.,
Электрохимия растворов, 3 изд., М., 1976; Мищенко К. П., Полторацкий Г.М., Термодинамика
и строение водных и неводных растворов электролитов, 2 изд., Л., 1976; Юхновский
И. Р., Головко М.Ф., Статистическая теория классических равновесных систем,
К., 1980; Ионная сольватация, М., 1987; Falkenhagen H., Theorie der Elektrolyte,
Lpz., 1971; The chemical physics of solvation, pt А, В, С, Amst., 1985-88. М. Ф. Головко. |
Поделитесь с друзьями:
Вы можете поставить ссылку на это слово:
будет выглядеть так: РАСТВОРЫ ЭЛЕКТРОЛИТОВ
будет выглядеть так: Что такое РАСТВОРЫ ЭЛЕКТРОЛИТОВ
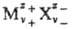 ,
состоящего из z+-валентных катионов
Mz+ и z_-валентных анионов X-, хим. потенциал равен:
,
состоящего из z+-валентных катионов
Mz+ и z_-валентных анионов X-, хим. потенциал равен: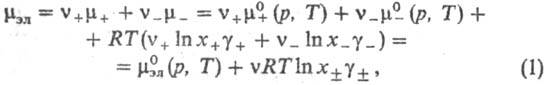
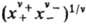 ,
g+ и g_ -коэффициенты активности катионов и
анионов,
,
g+ и g_ -коэффициенты активности катионов и
анионов, 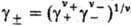 -средний
коэф. активности электролита
(см.
-средний
коэф. активности электролита
(см. 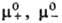 и
и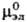 -стандартные
хим. потенциалы катионов,
анионов и электролита соотв., R-газовая постоянная.
-стандартные
хим. потенциалы катионов,
анионов и электролита соотв., R-газовая постоянная.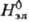 ,
,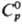 ,
,
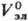 равны соответствующим
значениям для бесконечно разб. р-ра.
равны соответствующим
значениям для бесконечно разб. р-ра.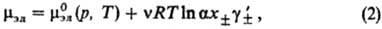
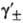 -средний
ионный коэф. активности. Степень диссоциации а находят из условия хим. равновесия,
к-рое в частном случае симметричного электролита (v+ =v_ = 1) приводит к ур-нию
для константы диссоциации KD (или константы ассоциации Ка):
-средний
ионный коэф. активности. Степень диссоциации а находят из условия хим. равновесия,
к-рое в частном случае симметричного электролита (v+ =v_ = 1) приводит к ур-нию
для константы диссоциации KD (или константы ассоциации Ка):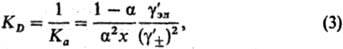
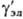 -
коэф. активности недиссоциир. молекул (для разбавленных Р.э.
-
коэф. активности недиссоциир. молекул (для разбавленных Р.э. 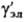 =
1). Аналогично (1) вводится также коэф. активности для р-рителя gS,
к-рый связан с ионными коэф. активности
=
1). Аналогично (1) вводится также коэф. активности для р-рителя gS,
к-рый связан с ионными коэф. активности 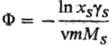
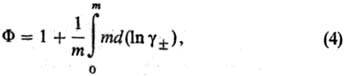
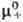 и
и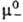 ,
коэф. активности g+ и g_ и связанные с ними парциальные
молярные величины м. б. определены только приближенно, на основе нетер-модинамич.
допущений (напр., о равенстве вкладов одинаковых по размерам и степеням окислений
катионов и анионов),
путем экстраполяции эксперим. данных для различных Р.э. с общим катионом или
анионом и др.
,
коэф. активности g+ и g_ и связанные с ними парциальные
молярные величины м. б. определены только приближенно, на основе нетер-модинамич.
допущений (напр., о равенстве вкладов одинаковых по размерам и степеням окислений
катионов и анионов),
путем экстраполяции эксперим. данных для различных Р.э. с общим катионом или
анионом и др.
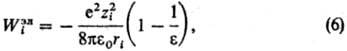
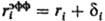 ,
где через di учитываются размеры молекул р-рителя. Предпринимаются
попытки моделирования р-рителя путем введения вместо e диэлектрич. ф-ции
и учета нелинейных диэлектрич. эффектов.
,
где через di учитываются размеры молекул р-рителя. Предпринимаются
попытки моделирования р-рителя путем введения вместо e диэлектрич. ф-ции
и учета нелинейных диэлектрич. эффектов. :
,):
:
,):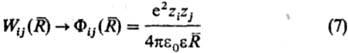
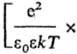
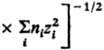 и радиусом Бьеррума
и радиусом Бьеррума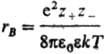 (k-пoстоянная
Больцмана, ni-плотность ионов i-го сорта). Первый из
них (rD) описывает расстояния, на к-рых экранируется поле
иона за счет образования облака ионов противоположного знака, второй (rB)-расстояния,
на к-рых кулоновское притяжение между катионом и анионом превышает среднюю энергию
теплового движения, что приводит к образованию ионных пар. Эффекты экранирования
кулоновских взаимод. учитываются
(k-пoстоянная
Больцмана, ni-плотность ионов i-го сорта). Первый из
них (rD) описывает расстояния, на к-рых экранируется поле
иона за счет образования облака ионов противоположного знака, второй (rB)-расстояния,
на к-рых кулоновское притяжение между катионом и анионом превышает среднюю энергию
теплового движения, что приводит к образованию ионных пар. Эффекты экранирования
кулоновских взаимод. учитываются 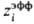 ,
в к-ром поправка di в явном виде зависит от диэлектрич.
проницаемости р-рителя и соотношения размеров иона и молекулы. Выражение для
диэлектрич. проницаемости удовлетворительно описывает эффект ее уменьшения при
увеличении концентрации ионов.
,
в к-ром поправка di в явном виде зависит от диэлектрич.
проницаемости р-рителя и соотношения размеров иона и молекулы. Выражение для
диэлектрич. проницаемости удовлетворительно описывает эффект ее уменьшения при
увеличении концентрации ионов.