Химическая энциклопедия
"ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ"
Главная - Химическая энциклопедия - буква Г - ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ химической технологии, подразделяют на процессы, протекающие с образованием неоднородных систем (диспергирование , перемешивание , псевдоожижение , пенообразование), с разделением этих систем (классификация гидравлическая , осаждение , фильтрование, центрифугирование и др.), с перемещением потоков в трубопроводах или аппаратах (см. Компрессорные машины , Насосы ). По условиям движения потоков различают след. задачи гидродинамики: 1)
внутреннюю-движение жидкостей и газов в трубопроводах и аппаратах, в т.
ч. в змеевиках, рубашках, трубном и межтрубном пространстве теплообменников,
ректификационных, экстракционных и абсорбционных колоннах, выпарных и сушильных
установках, печах; 2) внешнюю-движение частиц в газообразных и жидких средах,
включая осаждение пыли под действием силы тяжести в пылеосадительных камерах
или центробежной и инерц. сил в циклонах; разделение суспензий и эмульсий
в отстойниках, гидроциклонах, осадительных центрифугах и сепараторах; пневмо- и гидротранспорт
; барботирование
и перемешивание твердых частиц с жидкостями;
диспергирование жидкостей при распыливании в газовых и паровых средах (см. Газов очистка
, Циклоны
); 3) смешанную-движение жидкостей и газов через пористые
слои кусковых или зернистых материалов (см. Фильтрование
).
В последнем
случае в зависимости от высоты слоя материала Я различают процессы: а)
при H = = const-движение газа в абсорберах, регенеративных теплообменниках,
реакторах с неподвижным слоем катализатора (см. Реакторы химические
),
адсорберах, сушилках и печах; промывка осадков на фильтрах и др.; б)
при H Профили скоростей обусловлены формой сечения потока. Ур-ние движения интегрируют для разл. случаев, имеющих практич. применение (движение жидкости в узких каналах, кольцевом зазоре, пленке и др.). Для описания реальных процессов используют обобщенные ур-ния гидродинамики, приведенные к безразмерному виду с помощью подобия теории , а также типовые гидродинамич. модели (в зависимости от структуры потоков в аппаратах, в к-рых осуществляется процесс). Модель полного вытеснения характеризуется поршневым движением потоков при отсутствии продольного перемешивания (напр., в трубчатых аппаратах с >L/d > 20 при больших скоростях). Модель полного перемешивания отличается равномерным распределением частиц потока во всем объеме (напр., в реакторах с интенсивно работающей мешалкой). Промежут. модели (диффузионные, ячеечные) характеризуются частичным перемешиванием в продольном и радиальном направлениях. Движение твердых частиц в жидкости или газе (внеш. задача) описывается
с помощью упрощенных ур-ний Навье-Стокса (ползущее течение при Re <
1, течение в пограничном слое при больших числах Re). Закон сопротивления
выражается зависимостью Для описания процессов, составляющих смешанную задачу гидродинамики, используются упрощенные ур-ния Навье-Стокса с соответствующими граничными условиями. Закон сопротивления для неподвижного слоя зернистых материалов аналогичен ур-нию Дарси - Вейсбаха при замене d на dэ-эквивалентный диаметр межзерновых каналов. Г. п. разделения суспензий и аэрозолей (запыленных газов) фильтрованием (пропусканием через пористые перегородки, задерживающие дисперсную фазу) рассматривают отдельно. Теория фильтрования основана на эмпирич. законе Дарси. Перспективы развития Г. п. определяются совр. достижениями теоретич. и прикладной гидроаэродинамики и широким использованием методов моделирования и вычислит. техники. Лит.: Романков П. Г., Курочкина М. И., Гидромеханические процессы
химической технологии, 3 изд., Л., 1982. П. Г. Романков, М.И. Курочкина.
|
Поделитесь с друзьями:
Вы можете поставить ссылку на это слово:
будет выглядеть так: ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
будет выглядеть так: Что такое ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
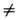 const -
фильтрование на пром. фильтрах и центрифугах. Осн. законы, к-рым подчиняется
движение жидкостей, газов и их смесей в трубах, каналах и аппаратах: сохранения
массы, энергии, кол-ва движения (импульса). Движение жидкости (газа) описывается
системой дифференц. ур-ний, включающей ур-ния движения Навье-Стокса и ур-ние
неразрывности (сплошности) потока. Интегрирование этого ур-ния приводит
к ур-нию постоянства расхода: V = f1w1= =
f2w2 =f3w3
(f1, f2, f3 - плошдди поперечных
сечений трубопровода, м2; w1, w2, w3-средние
скорости потока, м/с). Распределение скоростей по сечению канала зависит
от режима движения потока. При ламинарном режиме (наблюдается при умеренных
скоростях или в трубах малого диаметра) устанавливается параболич. профиль
скоростей (wcp = 0,5wмакс), при турбулентном режиме
(наблюдается при больших скоростях и сопровождается хаотич. пульсационными
движениями масс жидкости) wcp = = 0,817wмакс. Сопротивление
движению описывается ур-нием Дарси-Вейсбаха:
const -
фильтрование на пром. фильтрах и центрифугах. Осн. законы, к-рым подчиняется
движение жидкостей, газов и их смесей в трубах, каналах и аппаратах: сохранения
массы, энергии, кол-ва движения (импульса). Движение жидкости (газа) описывается
системой дифференц. ур-ний, включающей ур-ния движения Навье-Стокса и ур-ние
неразрывности (сплошности) потока. Интегрирование этого ур-ния приводит
к ур-нию постоянства расхода: V = f1w1= =
f2w2 =f3w3
(f1, f2, f3 - плошдди поперечных
сечений трубопровода, м2; w1, w2, w3-средние
скорости потока, м/с). Распределение скоростей по сечению канала зависит
от режима движения потока. При ламинарном режиме (наблюдается при умеренных
скоростях или в трубах малого диаметра) устанавливается параболич. профиль
скоростей (wcp = 0,5wмакс), при турбулентном режиме
(наблюдается при больших скоростях и сопровождается хаотич. пульсационными
движениями масс жидкости) wcp = = 0,817wмакс. Сопротивление
движению описывается ур-нием Дарси-Вейсбаха: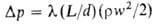 , где
, где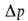 -потеря
давления на преодоление трения при движении потока в круглой цилиндрич.
трубе, L-длина трубы, d-ee диаметр,
-потеря
давления на преодоление трения при движении потока в круглой цилиндрич.
трубе, L-длина трубы, d-ee диаметр,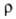 -плотность
жидкости,
-плотность
жидкости,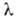 -коэф.
сопротивления, определяемый режимом потока и шероховатостью стенок трубы.
Для ламинарного режима
-коэф.
сопротивления, определяемый режимом потока и шероховатостью стенок трубы.
Для ламинарного режима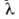 =
64/Re, где Re = =
=
64/Re, где Re = =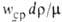 -число
Рейнольдса,
-число
Рейнольдса,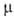 -динамич.
вязкость; для турбулентного режима
-динамич.
вязкость; для турбулентного режима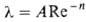 ,
где А и n-постоянные (для гидравлически гладких труб А = 0,316,
п = 0,25 в пределах Re от 4*103 до 105).
,
где А и n-постоянные (для гидравлически гладких труб А = 0,316,
п = 0,25 в пределах Re от 4*103 до 105).
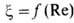 , где
, где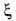 -коэф.
сопротивления. Для шарообразных частиц при Re < 1 величина
-коэф.
сопротивления. Для шарообразных частиц при Re < 1 величина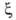 =
= 24/Re; при развитой турбулентности
=
= 24/Re; при развитой турбулентности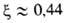 .
Скорость своб. осаждения под действием силы тяжести по закону Стокса для
одиночной шарообразной частицы woc = =
.
Скорость своб. осаждения под действием силы тяжести по закону Стокса для
одиночной шарообразной частицы woc = =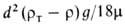 (при
(при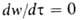 в
области 10-4 < Reoc < 2). Для приближенного
учета взаимного влияния частиц при стесненном осаждении суспензии в ф-лу
Стокса вводится поправка, зависящая от объемной доли жидкости в суспензии.
При расчете отстойников для сгущения суспензии различают режимы свободного
и стесненного осаждения. При действии центробежной силы осаждение твердой
фазы из жидкости или газа характеризуется центробежным числом Фруда-Fr
(т. наз. фактором разделения)-отношением центробежной силы Gц
к силе тяжести GT: Fru = Gц/Gт
=
в
области 10-4 < Reoc < 2). Для приближенного
учета взаимного влияния частиц при стесненном осаждении суспензии в ф-лу
Стокса вводится поправка, зависящая от объемной доли жидкости в суспензии.
При расчете отстойников для сгущения суспензии различают режимы свободного
и стесненного осаждения. При действии центробежной силы осаждение твердой
фазы из жидкости или газа характеризуется центробежным числом Фруда-Fr
(т. наз. фактором разделения)-отношением центробежной силы Gц
к силе тяжести GT: Fru = Gц/Gт
=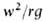 , где r-радиус
аппарата,
, где r-радиус
аппарата,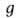 =9,81
м/с2. Для разделения суспензий в центробежном поле применяют
гидроциклоны и осадительные центрифуги, а для разделения пылегазовых систем-циклоны.
Эффективность работы последних характеризуется величиной
=9,81
м/с2. Для разделения суспензий в центробежном поле применяют
гидроциклоны и осадительные центрифуги, а для разделения пылегазовых систем-циклоны.
Эффективность работы последних характеризуется величиной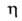 =
(c1
— c2)/c1, где с1и с2-концентрации
пыли в газе на входе в аппарат и выходе из него.
=
(c1
— c2)/c1, где с1и с2-концентрации
пыли в газе на входе в аппарат и выходе из него.