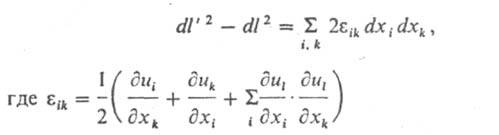Химическая энциклопедия
"ДЕФОРМАЦИЯ"
Главная - Химическая энциклопедия - буква Д - ДЕФОРМАЦИЯ
ДЕФОРМАЦИЯ
механическая (от лат. deformatio-искажение), изменение относит. расстояния между двумя произвольно выбранными точками в теле. В твердых телах Д. приводит к изменению формы или размеров тела целиком или его части, в жидкостях и газах - к течению. Осн. виды Д. - растяжение, сдвиг, кручение, изгиб, сжатие (одноосное или всестороннее). Термин "Д." относят как к процессу, протекающему во времени, так и к его результату, выражаемому величиной, к-рая характеризует относит. изменение размеров или формы любого мысленно выделенного элемента тела. Различают у п р у г у ю Д., полностью исчезающую после удаления вызвавшей ее нагрузки, п л а с т и ч е с к у ю, или Д. вязкого течения, к-рая остается после снятия вызвавшего ее внеш. воздействия; в я з к о у п р у г у ю, или запаздывающую, к-рая медленно и частично уменьшается после снятия нагрузки под действием протекающих в теле релаксац. процессов. Все реальные твердые тела, в к-рых доминируют упругие Д., обладают и пластич. св-вами. Однако обычно твердые тела можно считать упругими, пока нагрузка не превысит нек-рого предела; тогда тело либо разрушается, либо становится заметной пластич. Д. Для жидкостей определяющую роль играют пластич. Д., хотя всегда можно установить в них существование упругих Д. Для газов объемная Д. является упругой, а сдвиговая - необратимой.
Д. измеряют в относит. единицах. Для твердых тел, в к-рых доминируют упругие Д., в области достаточно малых Д. (порядка 0,1) выполняется Гука закон
. Для эластомеров характерны большие упругие Д., наз. высокоэластическими (см. Высокоэластическое состояние
); они достигают 8-12 единиц; пластич. Д. могут быть неограниченно велики.
Теория Д. основана на предположении о сплошности как тела в целом, так и его любых элементарных объемов. Пусть при Д. смещение нек-рой точки А с радиус-вектором r(х, у, z)в точку с радиус-вектором r (х, у, z) определяется вектором смещения u, так что r = r + и. Д. бесконечно малой окрестности к.-л. точки А определена, если известны изменения бесчисл. множества расстояний от этой точки до всех соседних точек. (Эти изменения расстояний определяют к тому же и изменения при Д. углов между направлениями от точки А к любым двум соседним точкам.)
Пусть радиус-вектор к.-л. соседней точки В есть r+dr, к-рый после Д. переходит в радиус-вектор r + dr, так что dr = dr+du. Расстояние от исходной точки А до соседней точки В перед Д. было: dl = (dr, dr)1/2, после Д. - dl = (dr, dr)1/2, так что dl2 = dl2 + 2(du, dr) + (du, du); скобки обозначают скалярное произведение векторов. При учете того, что du = S(дu/дxk)dxk, (x1 = х, х2 = y, х3 = z) из этого соотношения следует:
|
Поделитесь с друзьями:
Вы можете поставить ссылку на это слово:
будет выглядеть так: ДЕФОРМАЦИЯ
будет выглядеть так: Что такое ДЕФОРМАЦИЯ